写一个四则运算表达式转换成AST的方法
16 Sep 2019
Author:wuguanxi
0 前言
晓强哥在他的上篇文章里介绍了 Javascript 抽象语法树(https://wecteam.io/2019/07/19/Javascript抽象语法树上篇(基础篇)/)里面「提到获得抽象语法树的过程为:代码 => 词法分析 => 语法分析 => AST」,抱着深究技术细节的目的,我决定研究这里的词法分析和语法分析,写一个简单的四则运算表达式转换成AST的方法,于是就有了下面的内容。
1 人类和计算机对于表达式的看法是不同的
人类习惯 a + b 这种表达叫做「中序表达式」,优点是比较简单直观,缺点是要用一堆括号来确定优先级 (a + b) * (c + d)。
这里说简单直观是相对人类的思维结构来说的,对计算机而言中序表达式是非常复杂的结构。
为了计算机计算方便,我们需要将中序表达式转换成树形结构,也就是「抽象语法树AST」。
2 javascript 与抽象语法树 AST
我们知道,几乎任何语言中,代码在 "编译"(解释型语言在运行时也有编译的过程) 的过程中,都会生成一种树状的中间状态,这就是 AST。有些语言会直接把类似 AST 的语法暴露给程序员(例如:lisp、elixir、python等)。但是 javascript 并没有这个能力,但是我们可以用 javascript 自身实现这个过程。
获得抽象语法树的过程为:代码(字符串) => 词法分析(Lexer)=> Tokens => 语法分析(Parser) => AST
3 词法分析(Lexer)
词法分析有点像中文的分词,就是将字符串流根据规则生成一个一个的有具体意义的 Token ,形成 Token 流,然后流入下一步。
我们看一个简单的例子,
1 + 2.3
很明显这个表达式是可以分成三个 Token ,分别是 1 , + , 2.3。
词法分析这里,我们可以用有限状态机来解决。
3.1 有限状态机
绝大多数语言的词法部分都是用状态机实现的,我们下面就画出有限状态机的图形,然后根据图形直观地写出解析代码,总体图大概是这样。
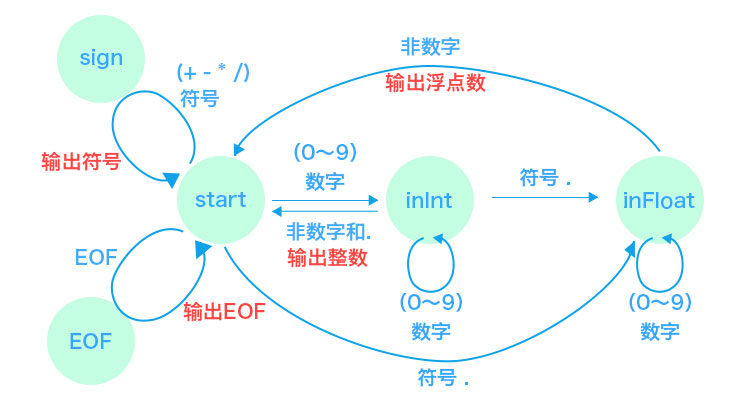
下面拆开细看。
3.2 开始(start)状态
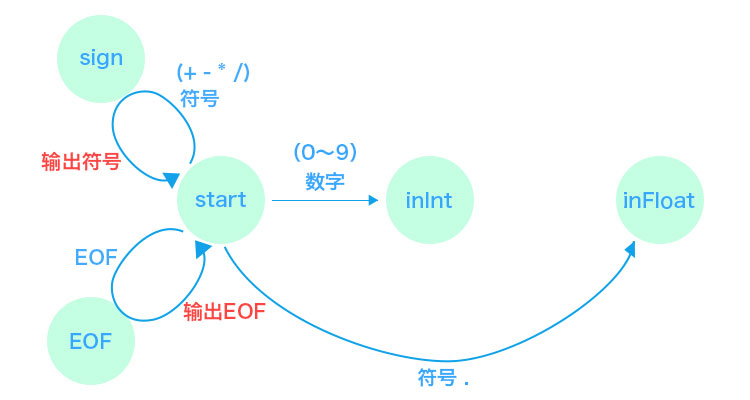
状态机的初始状态是 start 。
start 状态下输入数字(0 ~ 9)就会迁移到 inInt 状态。
start 状态下输入符号(.)就会迁移到 inFloat 状态。
start 状态下输入符号(+ - * /)就会输出 「符号 Token」 ,并回到 start 状态。
start 状态下输入 EOF 就会输出 「EOF Token」 ,并回到 start 状态。
代码大概是这个样子:
start(char) {
// 数字
if (["0","1","2","3","4","5","6","7","8","9"].includes(char)) {
this.token.push(char);
return this.inInt;
}
// .
if (char === "."){
this.token.push(char);
return this.inFloat;
}
// 符号
if (["+","-","*","/"].includes(char)) {
this.emmitToken("SIGN", char);
return this.start;
}
// 结束符
if (char === EOF){
this.emmitToken("EOF", EOF);
return this.start;
}
}
3.3 在整数(inInt)状态
start 状态下输入输入数字(0 ~ 9)就会迁移到 inInt 状态。
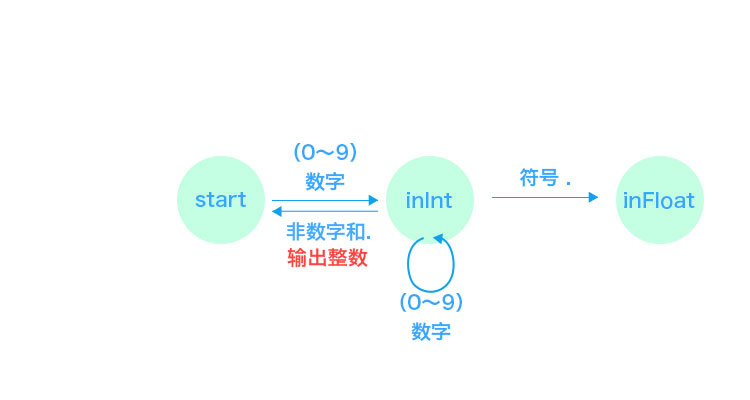
inInt 状态下输入输入符号(.)就会迁移到 inFloat 状态。
inInt 状态下输入数字(0 ~ 9)就继续留在 inInt 状态。
inInt 状态下输入非数字和.(0 ~ 9 .)就会就会输出 「整数 Token」 ,并迁移到 start 状态。
代码:
inInt(char) {
if (["0","1","2","3","4","5","6","7","8","9"].includes(char)) {
this.token.push(char);
return this.inInt;
} else if (char === '.') {
this.token.push(char);
return this.inFloat;
} else {
this.emmitToken("NUMBER", this.token.join(""));
this.token = [];
return this.start(char); // put back char
}
}
3.4 在浮点数(inFloat)状态
start 状态下输入符号(.)就会迁移到 inFloat 状态。
inInt 状态下输入输入符号(.)就会迁移到 inFloat 状态。
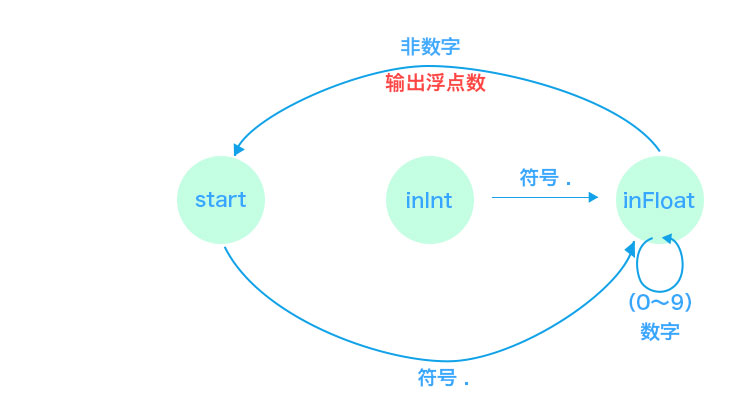
inFloat 状态下输入数字(0 ~ 9)就继续留在 inFloat 状态。
inFloat 状态下输入非数字(0 ~ 9 )就会就会输出 「浮点数 Token」,并迁移到 start 状态。
代码:
inFloat(char) {
if (["0","1","2","3","4","5","6","7","8","9"].includes(char)) {
this.token.push(char);
return this.inFloat;
} else if (char === ".") {
throw new Error("不能出现`..`");
} else {
if (this.token.length === 1 && this.token[0] === ".") throw new Error("不能单独出现`.`");
this.emmitToken("NUMBER", this.token.join(""));
this.token = [];
return this.start(char); // put back char
}
}
3.5 输出的 Token 种类 和定义
我将 「浮点数 Token」 和 「整数 Token」 合并为 [NUMBER Token] , 其他的 Token 还有 「SIGN Token」 和 「EOF Token」。
Token 的 定义:
interface Token{
type:String,
value:String,
}
3.6 完整的 Lexer 代码
const EOF = Symbol('EOF');
class Lexer {
constructor(){
this.token = []; // 临时 token 字符存储
this.tokens = []; // 生成的正式 token
// state 默认是 start 状态,后面通过 push 函数实现状态迁移
this.state = this.start;
}
start(char) {
// 数字
if (["0","1","2","3","4","5","6","7","8","9"].includes(char)) {
this.token.push(char);
return this.inInt;
}
// .
if (char === "."){
this.token.push(char);
return this.inFloat;
}
// 符号
if (["+","-","*","/"].includes(char)) {
this.emmitToken("SIGN", char);
return this.start;
}
// 结束符
if (char === EOF){
this.emmitToken("EOF", EOF);
return this.start;
}
}
inInt(char) {
if (["0","1","2","3","4","5","6","7","8","9"].includes(char)) {
this.token.push(char);
return this.inInt;
} else if (char === '.') {
this.token.push(char);
return this.inFloat;
} else {
this.emmitToken("NUMBER", this.token.join(""));
this.token = [];
return this.start(char); // put back char
}
}
inFloat(char) {
if (["0","1","2","3","4","5","6","7","8","9"].includes(char)) {
this.token.push(char);
return this.inFloat;
} else if (char === ".") {
throw new Error("不能出现`..`");
} else {
if (this.token.length === 1 && this.token[0] === ".") throw new Error("不能单独出现`.`");
this.emmitToken("NUMBER", this.token.join(""));
this.token = [];
return this.start(char); // put back char
}
}
emmitToken(type, value) {
this.tokens.push({
type,
value,
})
}
push(char){
// 每次执行 state 函数都会返回新的状态函数,实现状态迁移
this.state = this.state(char);
return this.check();
}
end(){
this.state(EOF);
return this.check();
}
check(){
// 检测是否有 token 生成并返回。
const _token = [...this.tokens];
this.tokens = [];
return _token;
}
clear(){
this.token = [];
this.tokens = [];
this.state = this.start;
}
}
const lexer = new lexer();
const input = `1 + 2.3`;
let tokens = [];
for (let c of input.split('')){
tokens = [...tokens,...lexer.push(c)];
}
tokens = [...tokens,...lexer.end()];
效果如下图:

自此,我们成功实现了词法分析,后面进入到语法分析。
4 语法分析(Parser)
前面的词法分析,已经将字符串划分成一个个有意义的 Token 进入到语法分析(Parser)。语法分析在编译原理里面属于比较高深的学问,我是没有怎么看懂。但总的来说就是把 Token流 组装成 AST , AST 的结构是既定的,后面我就通过对不同节点制定不同规则把 AST 组装起来。
4.1 定义 AST 结构 和 节点(Node)
简单来说 AST 就是一棵树形结构,由节点(Node)和 叶子(字面量 Literal )组成,节点 下面可以连接 其他节点 或者 字面量。最顶端的节点就是 根节点。

节点的定义就是一个简单的 javascript Object
interface Node {
type:string,
children:[],// children栈 里面可以是 Node 或者 Literal
maxChildren:number,
}
4.2 栈 和 根节点(Root)
语法分析(Parser)这里,我使用的是一个栈结构,每来一个 Token 就入栈,然后通过一定的规则组装 AST。
第一步就是压入 根节点 <Root>。
function RootNode(){
return {
type:"ROOT",
children:[],
maxChildren:0,
}
}
const stack = [RootNode()];

4.3 通用规则
在说明不同类型节点的规则前,先说一下通用规则。
-
- 没有后代的节点(NoChildrenNode),就是节点的 maxChildren 属性为 0。
-
- 非满的节点(NotFullNode),就是节点的 maxChildren 属性大于 0,而且其 children.length < maxChildren。
-
- 满的节点(FullNode),就是节点的 maxChildren 属性大于 0,而且其 children.length >= maxChildren。
对应的3个函数:
function isFullNode(node){
if (isNoChildrenNode(node)) return false;
return node && node.children && node.children.length >= node.maxChildren;
}
function isNotFullNode(node){
if (isNoChildrenNode(node)) return false;
return node && node.children && node.children.length < node.maxChildren;
}
function isNoChildrenNode(node){
return node.maxChildren === 0;
}
4.4 数字节点(Number)
定义一个数字节点,其children就是 数字字面量。
function NumberNode(){
return {
type:"NUMBER",
children:[...arguments],
maxChildren:1, // 只能有一个 child
}
}

4.5 数字节点的规则
-
- 找到栈顶 top
-
- 和数字节点 number
-
- top 不能是满项
-
- 如果 top 为非满的节点,number push 到 top.children
-
- 否则(top 是没有后代的节点),number 压栈
const top = stack[stack.length - 1]; // 栈顶
if (token.type === "NUMBER") {
// 1 1
// 1 + 1 1
if (isFullNode(top)) throw new Error("数字前一项不能是满项")
const number = CreateTypeNode(token.type)(token.value);
if (isNotFullNode(top)){
return topChildPush(number);
} else {
return stackPush(number);
}
}

4.6 符号节点(Sign + - * /)
定义一个符号节点,其 children 可以是 字面量 或者 其他节点。
function AddNode(){
return {
type:"+",
children:[...arguments],
maxChildren:2, // 能有两个 child
}
}
function SubNode(){
return {
type:"-",
children:[...arguments],
maxChildren:2, // 能有两个 child
}
}
function MulNode(){
return {
type:"*",
children:[...arguments],
maxChildren:2, // 能有两个 child
}
}
function DivNode(){
return {
type:"/",
children:[...arguments],
maxChildren:2, // 能有两个 child
}
}
4.7 节点的优先级
大家都知道,运算符有优先级,例如 * / 的优先级就比 + - 要高。我把这个优先级扩展到全部节点,所有节点都有一个优先级数值。
const operatorValue = {
"ROOT" : 0,
"+" : 1,
"-" : 1,
"*" : 2,
"/" : 2,
"NUMBER" : 3,
}
这个数值后面马上就会用到。
4.8 retire 操作
我们回到 1 + 2.3 这个算术表达式。前面说到 1 这个 Token 已经压入栈了,现在轮到 + Token 。
-
- 栈顶 top (就是 number 1)
-
- 符号节点 add
-
- top 是满的节点,所以 add 是后置符号,进入后置符号规则
-
- 比较 top 节点与 符号 add 节点 的优先级数值
-
- top < add 执行 rob 操作 ,否则 执行 retire 操作
// 后置符号
if (isFullNode(top)) {
if (operatorValue[token.value] > operatorValue[top.type]){
// 1 + 2 *
return rob(token.value,top.children);
} else {
// 1 +
// 1 + 2 +
link(token.value);
return retire(token.value);
}
}
先说 retire 操作,retire 有退休的意思。我是想表达,这当前条件下,栈顶节点可以退下来了,把栈顶的位置让给新节点。
步骤是把的旧栈顶节点出栈,新节点入栈,然后旧栈顶压进新节点的 children 栈里。
const retire = (type) => {
stack.push(CreateTypeNode(type)(stack.pop()));
}
然后到2.3 Token,根据前面的规则,因为栈顶的 add 节点是非满节点,2.3 构建成 number 节点 后,直接 push 到 add 节点的 children 栈里。
文字有点干,我们配合图一起看。

4.9 rob 操作
前面提到 retire 操作的反向条件是 rob 操作。先来看一个例子1 + 2.3 * 4。
接上一节,现在栈里是<Root>,<+ 1 2.3>,现需要压入新节点 mul,同样的 mul 节点和栈顶 add 节点比较, 优先级 mul > add,执行 rob 操作。
rob 操作 很好理解,因为乘法比加法的优先级要高,所以本来属于 add 节点 下的 number(2.3) 要被 mul 节点抢走了。
const rob = (type,children) =>{
const child = children.pop();
stack.push(CreateTypeNode(type)(child));
}
rob(token.value,top.children);
mul 节点抢走 number(2.3) 后放压进自己的 children 栈里,然后 mul 节点入栈,成为新的栈顶。
然后到4 Token,根据前面的规则,因为栈顶的 mul 节点是非满节点,4 构建成 number 节点 后,直接 push 到 mul 节点的 children 栈里。
文字还是有点干,我们配合图一起看。

4.10 link 操作
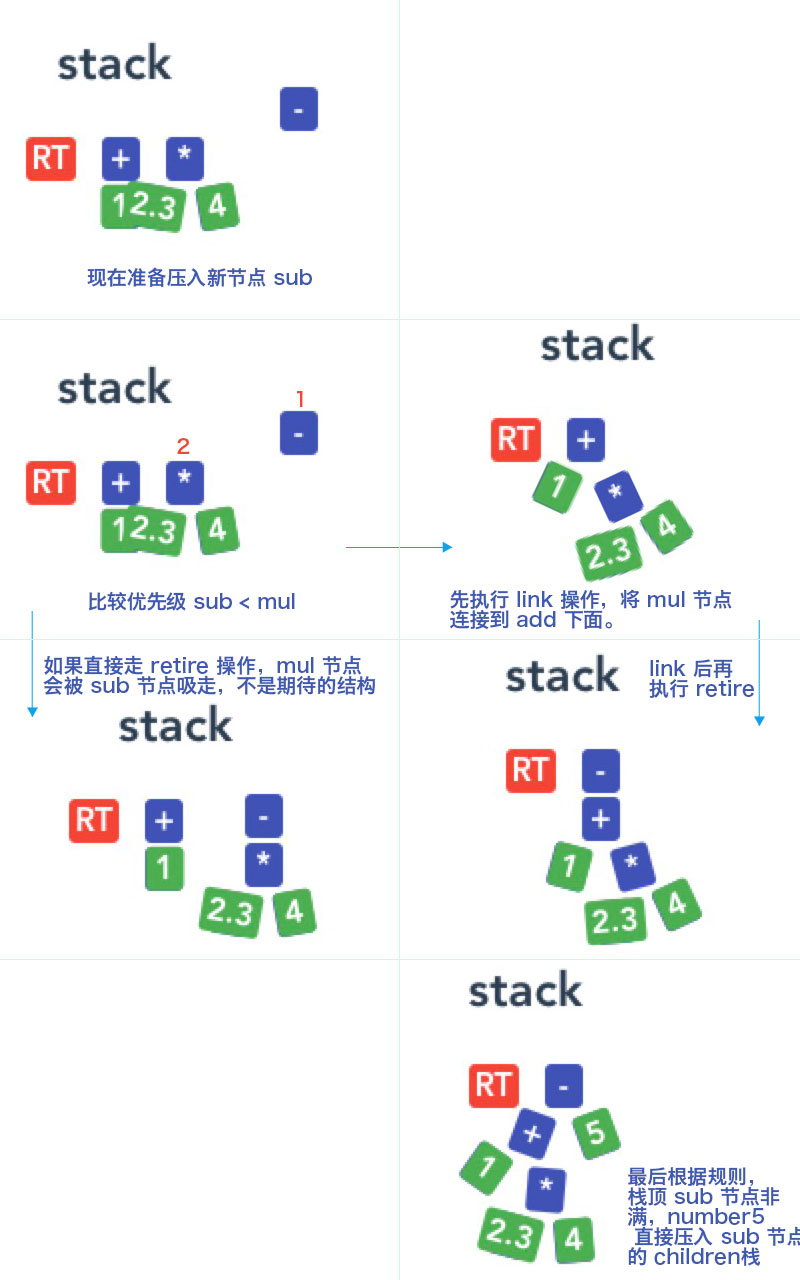
细心的朋友应该会发现,在执行 retire 操作之前还执行了一个 link 操作。这个 link 是做啥的呢?我们来看一个例子1 + 2.3 * 4 - 5。
接上一节,栈里现在是<Root>,<+ 1>,<* 2.3 4>,现在准备压入 sub 节点,因为优先级上 sub < mul ,如果先忽略 link 直接走 retire 操作,就会变成<Root>,<+ 1>,<- <* 2.3 4>>。这个不是我想要的结果,因为+和-优先级是相同的,相同优先级应该先计算先出现的符号,理想的操作下,栈里应该变成<Root>,<- <+ 1 <* 2.3 4>>>。所以我引入了 link 操作。
link 操作会先将栈顶的满项节点 push 到前一项的 childen 栈里(如果前一项是非满节点),而且这是一个循环操作 直到 前一项是满节点 或者 前一项节点的优先级比新节点的还要低。
回看上面的例子,栈里现在是 <Root>,<+ 1>,<* 2.3 4> ,现在准备压入 sub 节点,因为优先级上 sub < mul ,先在 link 操作下变成 <Root>,<+ 1 <* 2.3 4>> ,然后执行 retire ,
变成 <Root>,<- <+ 1 <* 2.3 4>>> 。
function typeValue(node){
if (node === undefined) throw new Error("node is undefined");
return operatorValue[node.type];
}
const link = (type) =>{
const value = operatorValue[type];
while(isFullNode(stack[stack.length -1]) && isNotFullNode(stack[stack.length - 2]) && (value <= typeValue(stack[stack.length -1])) && (value <= typeValue(stack[stack.length -2])) ) {
stack[stack.length - 2].children.push(stack.pop());
}
}
然后到 5 Token,根据前面的规则,因为栈顶的 sub 节点是非满节点,5 构建成 number 节点 后,直接 push 到 mul 节点的 children 栈里。
继续上图。
4.13 增加负数
负数可以说是开了一个比较坏的先河,因为和减号公用一个 - 符号,导致代码逻辑的增加。负号和减号的区别在于,负号的取值是在它的右侧 1 + - 1 ,减号是从左到右 1 - 1 。这里可以通过判断栈顶节点的情况来确定究竟是 负号 还是 减号。我将 负号这种取值在右边的符号称为 前置符号 ,加减乘除这种左到右取值的符号称为 后置符号。前置符号直接压栈。
// 定义负数节点
function NegNode(){
return {
type:"NEGATE",
children:[...arguments],
maxChildren:1,
}
}
if (token.type === "SIGN") {
// 后置符号
if (isFullNode(top)) {
if (operatorValue[token.value] > operatorValue[top.type]){
// 1 + 2 *
// console.log("rob");
return rob(token.value,top.children);
} else {
// 1 +
// 1 + 2 +
link(token.value);
return retire(token.value);
}
}
// 前置符号
if (
(isNoChildrenNode(top)) || // (-
(isNotFullNode(top)) // 1 + -
){
if (token.value === "-") return stackPush(CreateTypeNode("NEGATE")()); // 取负公用符号 -
if (token.value === "+") return ; // + 号静默
throw new Error(token.value + "符号不能前置");
}
}
例子 - 1 。 - 1 这里开始栈 <Root> ,然后准备压入 - ,因为 Root 节点是没有后代的节点(NoChildrenNode),所以这里判断-是前置符号,生成 NE(NEGATE) 节点直接入栈 <Root><NE> 。然后是 1 , <Root><NE 1> 。
例子 1 - - 1 。这里第一个 - 时 <Root><1> ,因为 栈顶 number 节点是满的节点(FullNode),所以第一个 - 是后置符号,生成 sub 节点。第二个 - 时 <Root><- 1>,
栈顶的 sub 节点是未满的节点(NotFullNode),判定为前置符号,生成 NE(NEGATE) 节点直接入栈 <Root><- 1><NE> 。然后是 1 , <Root><- 1><NE 1> 。

4.14 增加括号
括号 ( 可以改变表达式里的优先级,先定义括号节点。
首先需要在 词法分析 的时候加入 ( 。
// start 状态里
// 符号
if (["+","-","*","/","("].includes(char)) {
this.emmitToken("SIGN", char);
return this.start;
}
function ParNode(){
return {
type:"(",
children:[],
maxChildren:0,
}
}
这里 maxChildren 设为 0 ,当我们将 括号节点 push 到栈里时,就形成一个屏障,使后面节点变动时,不会越过 括号节点 。
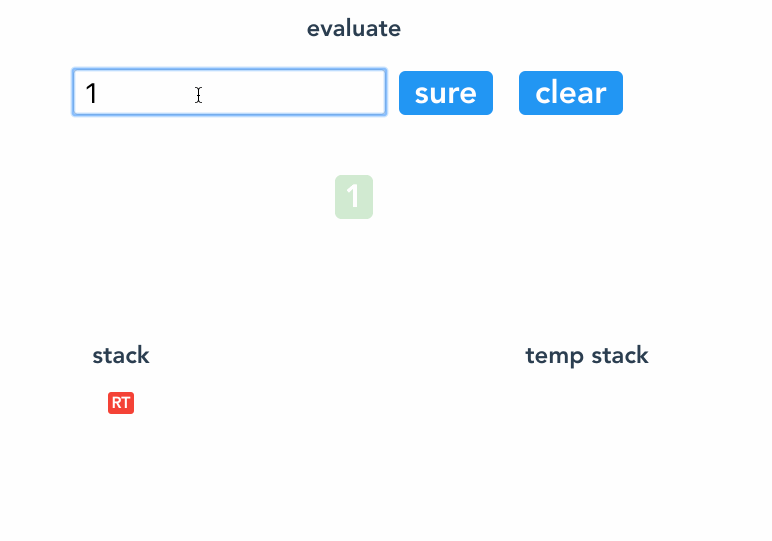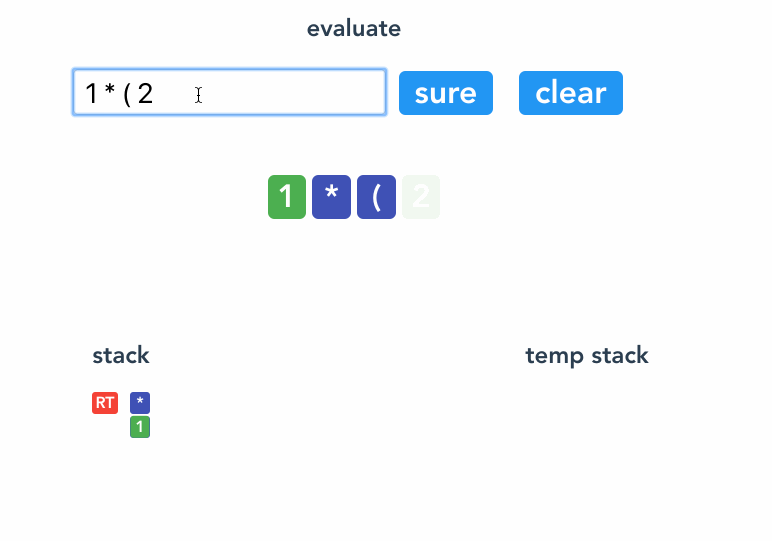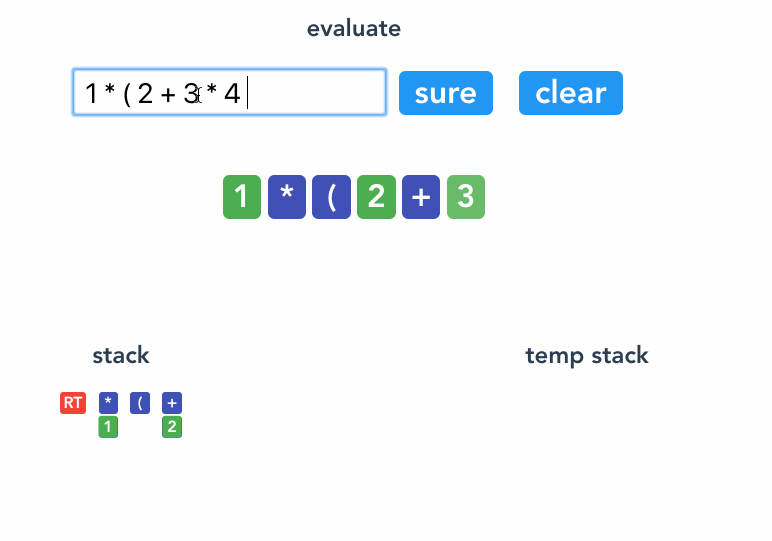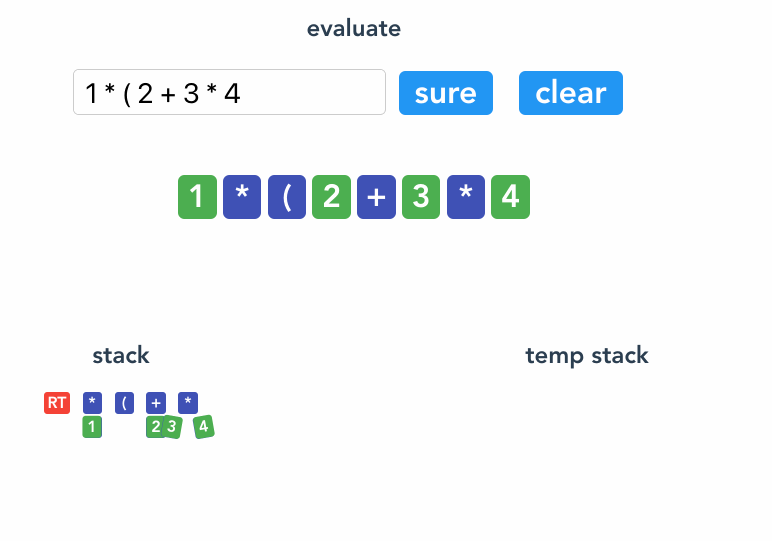
看例子 1 * (2 + 3 * 4) 。
`<Root>`
1 `<Root><1>`
* `<Root><* 1>`
( `<Root><* 1><(>` // ( 隔离
2 `<Root><* 1><(><2>` // 把 2 和 * 隔离
+ `<Root><* 1><(><+ 2>`
3 `<Root><* 1><(><+ 2 3>`
* `<Root><* 1><(><+ 2><* 3>`
4 `<Root><* 1><(><+ 2><* 3 4>`
参考代码。
if (token.value === "(" ) {
// 1(
// 1 + 1 (
if (isFullNode(top)) throw new Error("not a function");
// (
return stackPush(CreateTypeNode("(")());
}
4.14 增加反括号 与 remove 操作
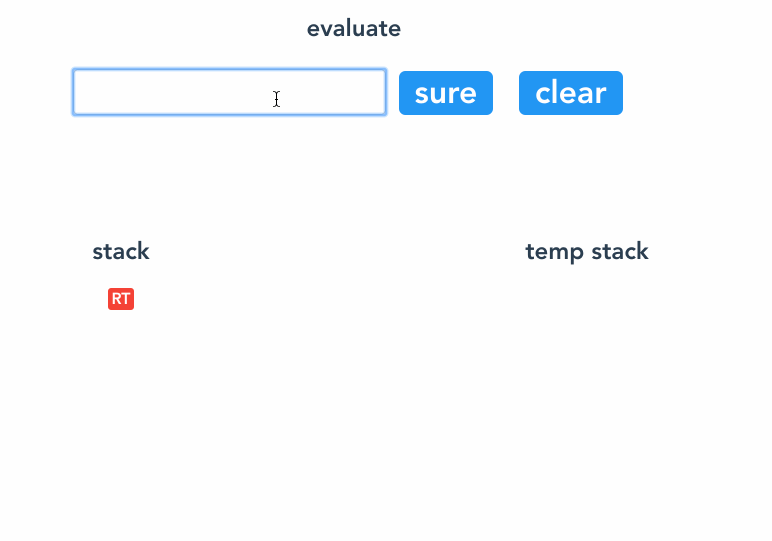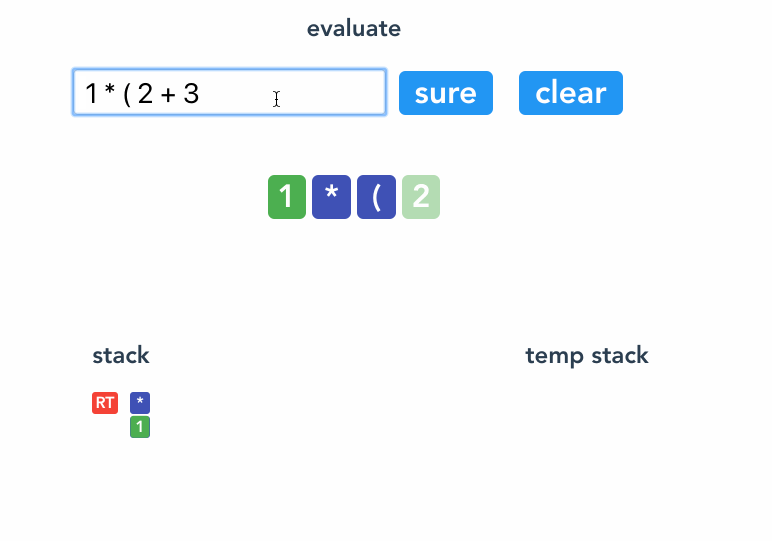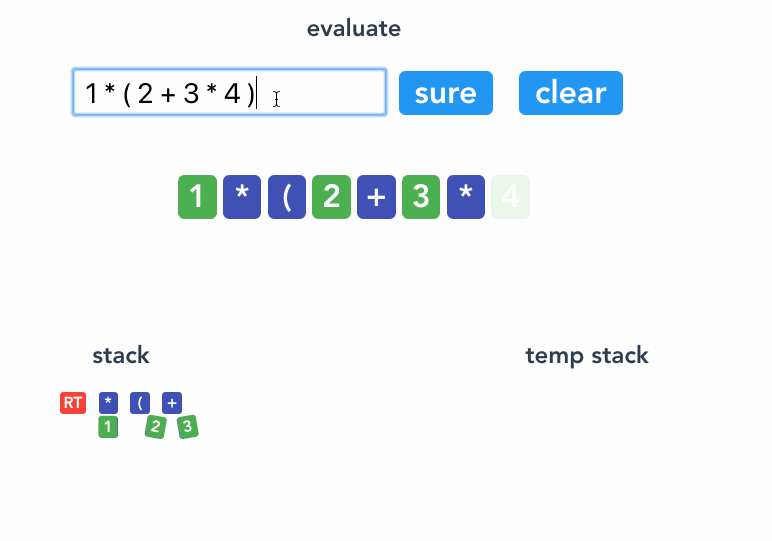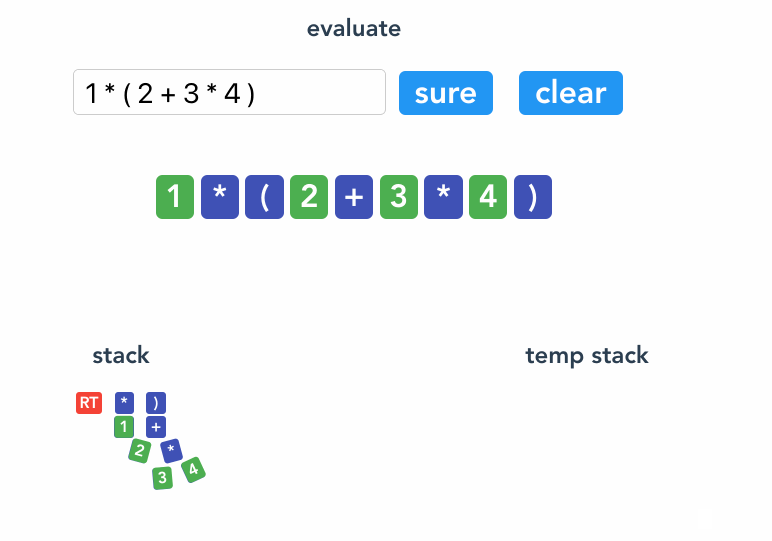
反括号 ) 的作用是将当前括号后面添加的节点收缩成一个稳定节点,具体方法是把 ( 后面的节点 link 起来( ( 的优先级设定得比较小,旨在将括号里的节点都连接起来),并推到一个临时的栈里,然后将 ( 节点 改写成 ) 节点 ,再将临时栈的节点出栈 push 到 ) 节点的 children 里。还因为 ) 节点的优先级别设置了很高,不用担心会被后面的节点 rob 。
首先需要在 词法分析 的时候加入 ) 。
// start 状态里
// 符号
if (["+","-","*","/","(",")"].includes(char)) {
this.emmitToken("SIGN", char);
return this.start;
}
if (token.value === ")" ) {
// ()
if (isNoChildrenNode(top)) throw new Error("Unexpected token )");
// (1+)
if (isNotFullNode(top)) throw new Error("Unexpected token )");
return remove("("); // 收拢 (
}
const remove = (type) => {
link(type);
// 找到最近的( 其余push到tempStack
while(stack.length > 0 && !(stack[stack.length - 1].type === type && !stack[stack.length - 1].children)){
tempStack.push(stack.pop());
}
// 修改最近的(
const top = stack[stack.length - 1];
if (top.type === type){
top.type = opposite[type]; // 取反 ( => )
top.children = [];
// tempStack的Node压给(
while(tempStack.length > 0){
top.children.push(tempStack.pop());
}
top.maxChildren = top.children.length; // maxChildren 设满
}
}
const operatorValue = {
"ROOT" : 0,
"(" : 1, // 括号的优先级低,方便 link
"+" : 2,
"-" : 2,
"*" : 3,
"/" : 3,
"NEGATE" : 4, // 取负
"NUMBER" : 5, // 取正
")" : 6, // 反括号的优先级高,防止被 rob
"ROOT_END" : 7,
}
const opposite = {
"(" : ")" ,
"ROOT" : "ROOT_END",
}
4.15 EOF
括号的作用是将其内部的节点包裹起来,形成一个稳定的节点,括号 ( 和反括号 ) 自成一对。还有一对有同样的功能,就是 ROOT 和 ROOT_END 。
ROOT 和 ROOT_END 标示着这个表达式的开始和结束。 ROOT 节点是初始化时就添加的,那么 ROOT_END 对应就是 EOF 这个 Token 了。
if (token.type === "EOF") {
// EOF
return remove("ROOT");
};
来一个完整的流程gif。
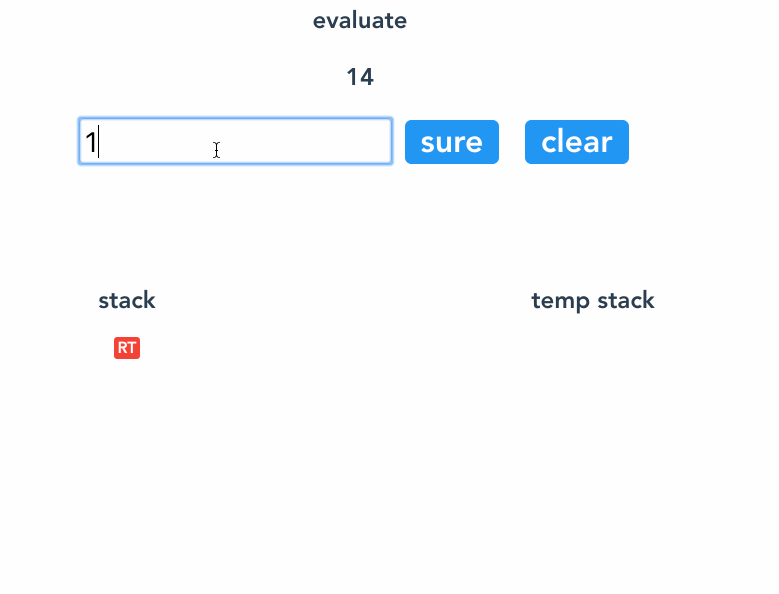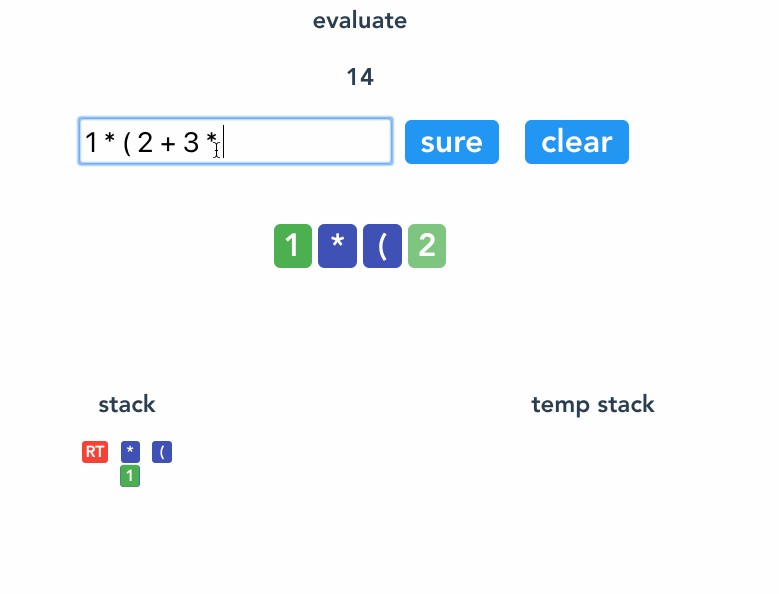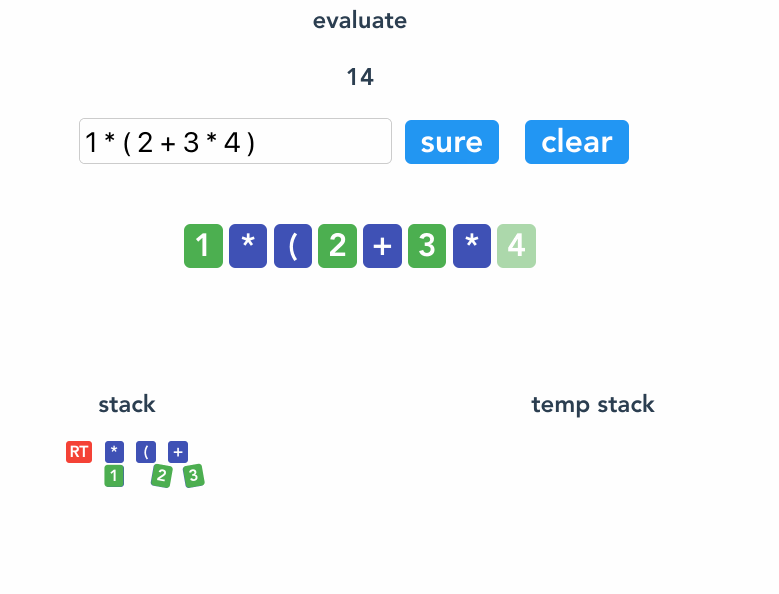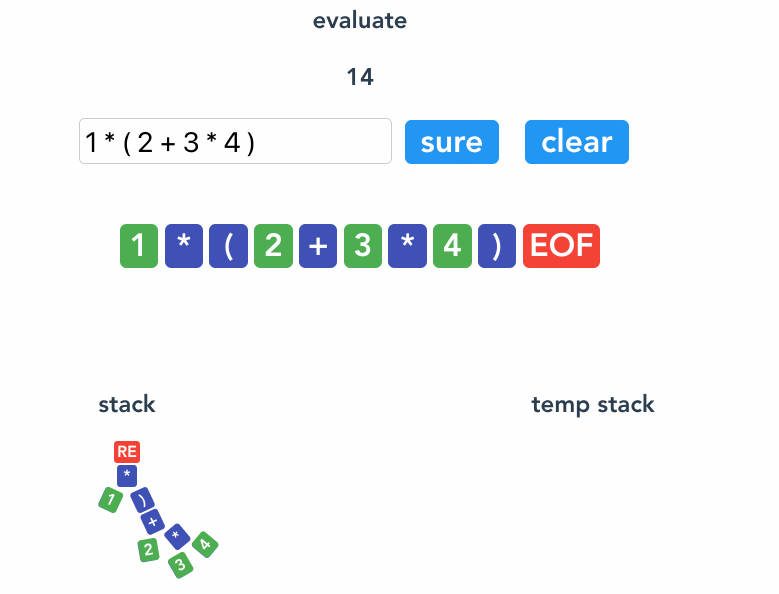
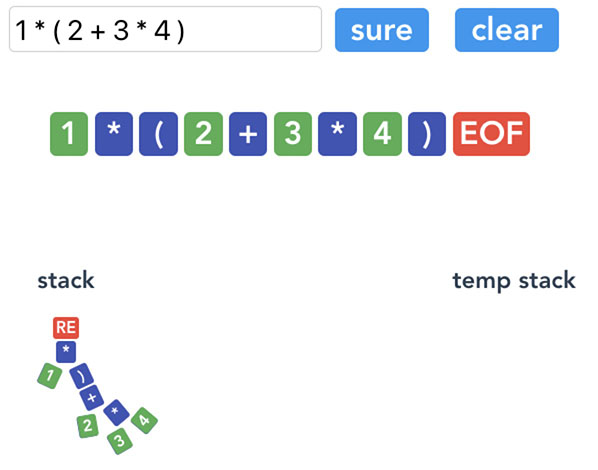
5 计算求值
EOF 后,我们就可以得到抽象语法树 AST 了。因为是树形结构,我们可以用递归的方法求值。
`1 * ( 2 + 3 * 4)`
const ast = {
"type": "ROOT_END",
"children": [{
"type": "*",
"children": [{
"type": "NUMBER",
"children": ["1"],
}, {
"type": ")",
"children": [{
"type": "+",
"children": [{
"type": "NUMBER",
"children": ["2"],
}, {
"type": "*",
"children": [{
"type": "NUMBER",
"children": ["3"],
}, {
"type": "NUMBER",
"children": ["4"],
}],
}],
}],
}],
}],
}
function evaluate(node){
const {type,children} = node;
if (type === "NUMBER") return Number(children[0]);
if (type === "+") return evaluate(children[0]) + evaluate(children[1]);
if (type === "-") return evaluate(children[0]) - evaluate(children[1]);
if (type === "*") return evaluate(children[0]) * evaluate(children[1]);
if (type === "/") return evaluate(children[0]) / evaluate(children[1]);
if (type === ")") return evaluate(children[0]);
if (type === "ROOT_END") return evaluate(children[0]);
if (type === "NEGATE") return evaluate(children[0]) * -1;
}
console.log(evaluate(ast)); // 14
6 小结
写到这里,一个简单的四则运算解析器总算完成了。一共分 3 大部分。分别是 词法分析(Lexer)、语法分析(Parser)、计算求值(evaluate)。
词法分析(Lexer)是将 表达式 字符串 转化为 Token 流,这里用到有限状态机。
语法分析(Parser)是将 Token 流 转化为 抽象语法树(AST),这里主要是手工写的语法分析,用了 两个栈 ,规定了 4 个方法 link 、 retire 、 rob 、 remove,还有定义了不同节点的入栈规则。
计算求值(evaluate)是将 AST 计算出表达式的 值,这里用了递归求值。
7 应用之自定义的向量运算
弄清楚四则运算的解析方法后,我们可以创造自己制定规则的表达式运算了。
因为之前的项目我写过向量运算,但是因为函数调用的写法有点丑陋,我这里就尝试自定义向量运算表达式。
7.1 向量表示之引入符号(Sign [ , ])
这里一个 2维向量 我用 [1,2] 来表示。所以先在 词法分析(Lexer)里增加 [,] 。
// start 状态里
// 符号
if (["+","-","*","/","(",")","[",",","]"].includes(char)) {
this.emmitToken("SIGN", char);
return this.start;
}
[ 和 ] 是一对,本质和括号对 ( ) 没什么区别。
, 其定位就是一个分割符,没有成对子。而且 , 出现后,其前面的节点都要 link 起来。
function VecNode(){
return {
type:"[",
children:[],
maxChildren:0,
}
}
function WallNode(){
return {
type:",",
children:[],
maxChildren:0,
}
}
const opposite = {
"(" : ")" ,
"[" : "]" ,
"ROOT" : "ROOT_END" ,
}
if (token.value === "[" ) {
// 1[
// 1 + 1 [
if (isFullNode(top)) throw new Error("非顶端[前面不能有满项");
return stack.push(CreateTypeNode("[")());
}
if (token.value === "," ) {
// ,
// ,,
// (,
// [,
if (isNoChildrenNode(top)) throw new Error(",不能接在空符后面");
// [ 1 + ,
if (isNotFullNode(top)) throw new Error(",不能接在非满项后面");
link("[");
return stack.push(CreateTypeNode(",")());
}
if (token.value === "]" ) {
// [1+]
if (isNotFullNode(top)) throw new Error("]前不能有非满项");
return remove("[");
}
例子 [ 1 + 2 * 3 , 4 + 5 * 6 ] 。
`<Root>`
[ `<Root><[>`
1 `<Root><[><1>`
+ `<Root><[><+ 1>`
2 `<Root><[><+ 1 2>`
* `<Root><[><+ 1><* 2>`
3 `<Root><[><+ 1><* 2 3>`
, `<Root><[><+ 1 <* 2 3>><,>`
4 `<Root><[><+ 1 <* 2 3>><,><4>`
+ `<Root><[><+ 1 <* 2 3>><,><+ 4>`
5 `<Root><[><+ 1 <* 2 3>><,><+ 4 5>`
* `<Root><[><+ 1 <* 2 3>><,><+ 4><* 5>`
6 `<Root><[><+ 1 <* 2 3>><,><+ 4><* 5 6>`
] `<Root><[><+ 1 <* 2 3>><,><+ 4<* 5 6>>`
`<Root><] <+ 1 <* 2 3>><,><+ 4<* 5 6>>>`
EOF `<RootEnd <] <+ 1 <* 2 3>><,><+ 4<* 5 6>>>>`
最后在 evaluate 方法里增加对向量的支持。
// evaluate 里
if (type === "]") {
const notWall = children.filter(item => item.type !== ",");
const a = evaluate(notWall[0]);
const b = evaluate(notWall[1]);
const isNumA = typeof a === "number";
const isNumB = typeof b === "number";
if (isNumA && isNumB) {
return new Vector2d(a,b);
} else {
throw new Error("只有两个数量才能生成向量");
}
}


7.2 向量加减乘除法取负
向量加减乘除法取负继续源用 + , - , * , / 符号,只需要在 evaluate 方法里做判断就可以了。
// evaluate 里
if (type === "+") {
const a = evaluate(children[0]);
const b = evaluate(children[1]);
if (Vector2d.is(a) && Vector2d.is(b)){
return Vector2d.add(a,b);
} else {
return a + b;
}
}
if (type === "-") {
const a = evaluate(children[0]);
const b = evaluate(children[1]);
if (Vector2d.is(a) && Vector2d.is(b)){
return Vector2d.sub(a,b);
} else {
return a - b;
}
}
if (type === "*" || type === "/") {
const a = evaluate(children[0]);
const b = evaluate(children[1]);
const isVecA = Vector2d.is(a);
const isVecB = Vector2d.is(b);
const isNumA = typeof a === "number";
const isNumB = typeof b === "number";
if ( isNumA && isNumB ){
if (type === "*") return a * b;
if (type === "/") return a / b;
} else if(isVecA && isNumB) {
if (type === "*") return Vector2d.scale(a,b);
if (type === "/") return Vector2d.scale(a,1/b);
} else if (isVecB && isNumA) {
if (type === "*") return Vector2d.scale(b,a);
if (type === "/") return Vector2d.scale(b,1/a);
} else {
throw new Error("两个向量不能相乘,请用@dot");
}
}
if (type === "NEGATE") {
const a = evaluate(children[0]);
if (Vector2d.is(a)){
return Vector2d.scale(a,-1);
} else {
return a * -1;
}
}
7.3 向量旋转、点乘,角度的单位转换
向量的旋转(@rot)、点乘(@dot),角度的单位转换(@deg),用这3个自定义符号。
这里需要修改一下 词法分析 的状态机,在 start 状态下新增一个跃迁状态 customSgin 用 @ 为标识。然后 customSgin 状态下输入[a-zA-Z]都回跃迁自身 否则 跃迁回状态 start 并输出 Token。

// Lexer 里
start(char) {
// 数字
if (["0","1","2","3","4","5","6","7","8","9"].includes(char)) {
this.token.push(char);
return this.inInt;
}
// .
if (char === "."){
this.token.push(char);
return this.inFloat;
}
// 符号
if (["+","-","*","/","(",")","[","]",",","<",">"].includes(char)) {
this.emmitToken("SIGN", char);
return this.start
}
// 空白字符
if ([" ","\r","\n"].includes(char)) {
return this.start;
}
// 结束
if (char === EOF){
this.emmitToken("EOF", EOF);
return this.start
}
if (char === "@"){
this.token.push(char);
return this.customSgin;
}
}
customSgin(char) {
if ("abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ".split("").includes(char)) {
this.token.push(char);
return this.customSgin;
} else {
this.emmitToken("SIGN", this.token.join(""));
this.token = [];
return this.start(char); // put back char
}
}
然后定义节点和节点优先级。
function DegNode(){
return {
type:"@deg",
children:[...arguments],
maxChildren:1,
}
}
function DotNode(){
return {
type:"@dot",
children:[...arguments],
maxChildren:2,
}
}
function RotNode(){
return {
type:"@rot",
children:[...arguments],
maxChildren:2,
}
}
const operatorValue = {
"ROOT" : 0,
"(" : 1,
"[" : 1,
"@dot" : 2, // 向量点乘
"<" : 3,
">" : 3,
"+" : 4,
"-" : 4,
"*" : 5,
"/" : 5,
"@rot" : 5, // 向量旋转
"NEGATE" : 6, // 取负
"@deg" : 7, // 角度转换
"NUMBER" : 8, // 取正
")" : 9,
"]" : 9,
"ROOT_END" : 10,
}
还有在 evaluate 里写对应的方法。
if (type === "@dot"){
const a = evaluate(children[0]);
const b = evaluate(children[1]);
const isVecA = Vector2d.is(a);
const isVecB = Vector2d.is(b);
if (isVecA && isVecB) {
return Vector2d.dot(a,b);
} else {
throw new Error("只有向量和向量能点乘");
}
}
if (type === "@rot"){
const a = evaluate(children[0]);
const b = evaluate(children[1]);
const isVecA = Vector2d.is(a);
const isVecB = Vector2d.is(b);
const isNumA = typeof a === "number";
const isNumB = typeof b === "number";
if (isVecA && isNumB) {
return Vector2d.rotate(a,b);
} else if (isVecB && isNumA) {
return Vector2d.rotate(b,a);
} else {
throw new Error("只有向量和数量能旋转");
}
}
if (type === "@deg"){
const a = evaluate(children[0]);
const isNumA = typeof a === "number";
if (isNumA){
return a / 180 * Math.PI;
} else {
throw new Error("非数字不能转换deg");
}
}
来一个例子 [1, 0] @rot - 90 @deg ,把 [1,0] 旋转负 90 度。

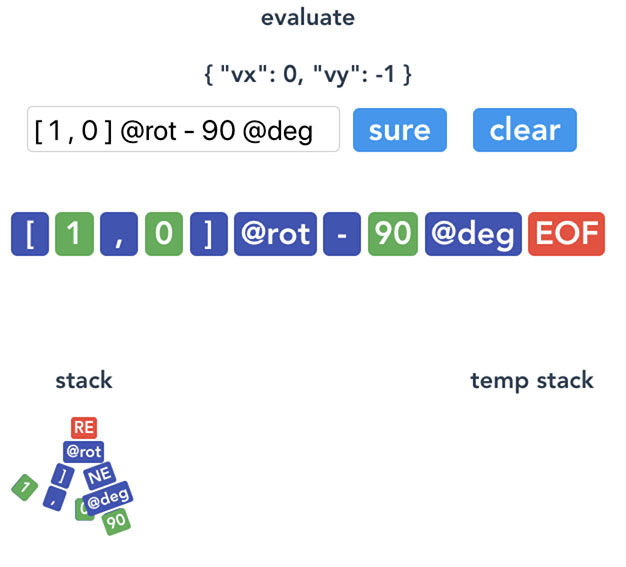
8 Demo手动玩
最后结合 Vue 写了一个 表达式转 AST 的可视化 demo,支持数字和向量。